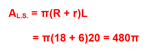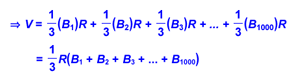Printable version

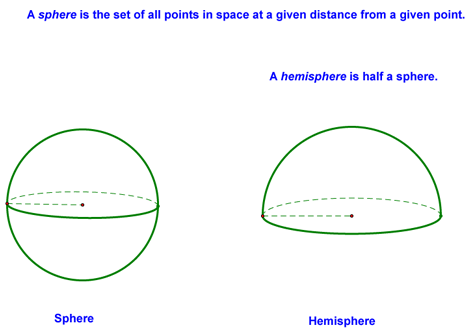
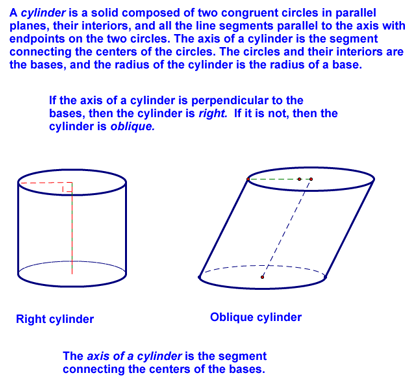
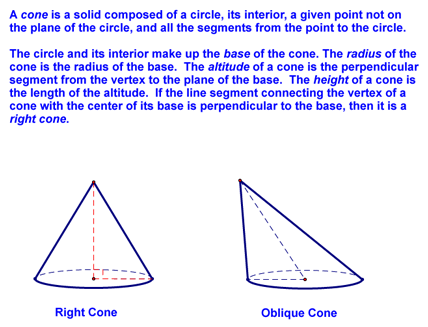
Surface Area of Circular Solids - Lesson 12-3

Today we talked about the surface area of circular solids. We started by defining spheres, hemispheres, cylinders, and cones:

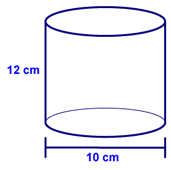
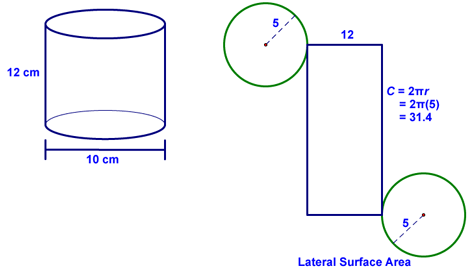
After doing this, we looked at the following examples. First, we looked at finding the surface area of the following cylinder:

In order to do this, we "unwrapped" the cylinder to look like:

From this, we were able to calculate the surface area. The only complicated part is to recognize that the "width" (assuming that the height is 12) of the rectangle that forms the lateral surface area is the circumference of the circular bases.

This problem can be summarized in the following theorem:

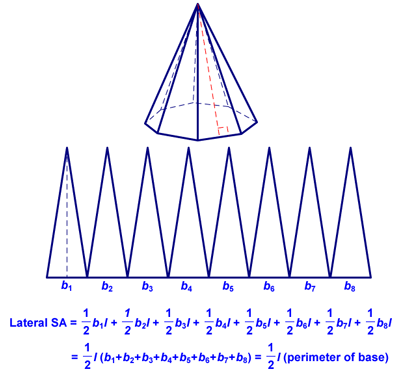
Next we derived the formula for the surface area of a cone. We started by thinking about how to find the lateral area of an octagonal pyramid:

We then thought about how this would work if we increase the number of sides of the base to 10, 20, 100, or 1,000,000...it would get closer and closer to the lateral surface area of a cone, right? The perimeter of the base would get closer and closer to the circumference of the circular base, right? From this, we came up with the following theorem:

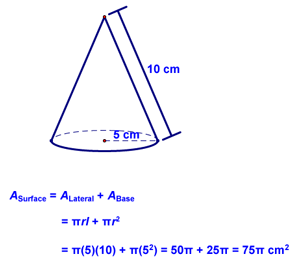
We did the following example using this new theorem:

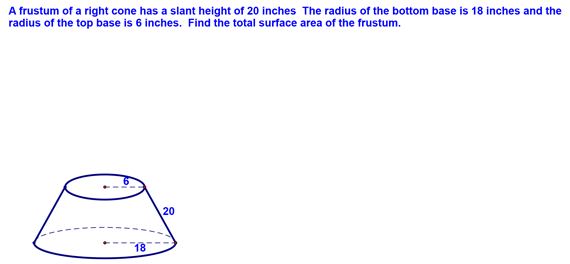
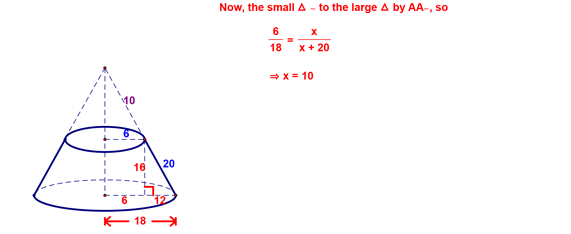
Next, we talked about how to find the surface area of a frustum, which I liked to a gear. A frustum is the solid left when you take away the top part of a cone (see the diagram below). For our example, we did the following:

We started by showing how this frustum was made by taking away the top part of a cone. When we drew this in, we saw we had similar triangles and were able to determine a number of lengths based on this:

We next looked at finding the value of x, the slant height of the cone cut out to form the frustum. This was done using a proportion we set up based on the similar triangles:

From here, we were able to calculate the surface area:

Before moving on from frustums, I wanted to show you a method for determining the lateral surface area that is sometimes simpler than subracting the lateral area of the smaller cone from the lateral area of the larger cone. The derivation shown below is a little complex, but the end result is nice...

We started with a frustum labeled as shown:

Next, we drew in the "missing cone" and did some labeling:

From here, we used similar triangles to find values for L₁ and L₂:

From here, we used the same approach as in the previous example, did some simplification and came up with a new formula:

So, to find the lateral area of the first example we did, all we need to do using this formula is:

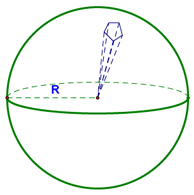
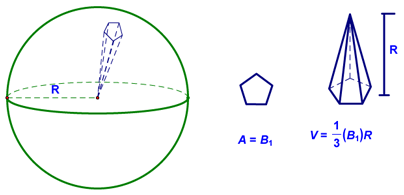
You can choose to use this formula or not...it's up to you. You can always just subtract the lateral area of the smaller cone from the lateral area of the larger one to find the lateral area of the frustum, as we did in our first example.

We then talked about how to derive the formula for the surface area of a sphere. We started with a sphere and imagined breaking it up into 1000 "sort-of" polygons:

Each of these is a pyramid with a volume as shown below:

We then noted that the surface area of the sphere would be the sum of the area of the 1000 bases of the pyramids:

We also noted that the volume of the sphere would be the sum of the volumes of the 1000 pyramids (from which we could factor out the surface area):

Now, using the formula for the volume of a sphere, we are able to derive a formula for the surface area:

This is summarized by the following postulate: